Digging into Factor Analysis

Hi Everyone!!
I finally found some time alone to sit down and pen an introductory article on factor analysis. So here goes!
At a fundamental level Factor Analysis (FA) is a data reduction tool. It tries to look for patterns in observable data to uncover hidden or ‘latent’ variables. The question that marketers need to ask is ‘how?’.
There are two answers to that question. The simple one - FA tries to filter our redundant data by isolating correlated variables and clubbing them together. What remains is the essence of the latent variable. The complex one involves some math. But let me try and explain it so that you have an idea of what really goes on when you perform FA.
Imagine the following. Let’s have some quantitative measures of all the students in our class. What sort of variables might they be?
- Participation in clubs (x₁)
- Leadership initiatives (x₂)
- Group scores in exams (x₃)
- Time spent working in groups (x₄)
- Number of different teams one is involved in (x₅)
- Individual scores in exams (x₆)
- Class participation scores (x₇)
- Attendance records (x₈)
- Participation in placement activities (x₉)
- Number of complains against individual (x₁₀)
The list may go on. However, it is somewhat possible for one to think that some of these scores do in fact measure the same underlying latent variables. For instance, I may be able to think of x₁ to x₅ as variables that capture one’s team work potential. Similarly, x₆ and x₇ may be argued to capture one’s intellectual ability and x₈ to x₁₀ are are all variables that capture one’s discipline.
As you can see, at the moment, all I’m doing is guessing.
If I really don’t know what underlying variables are there to begin with, and I’m trying to ‘explore’ through the FA, then I am said to be involved in Exploratory Factor Analysis or EFA. Let’s talk about just that part now.
Let’s say we do not know what these ‘factors’ or ‘latent’ variables are. Let’s just call them F₁, F₂, F₃ and so on. Could I theoretically specify regression equations like these:
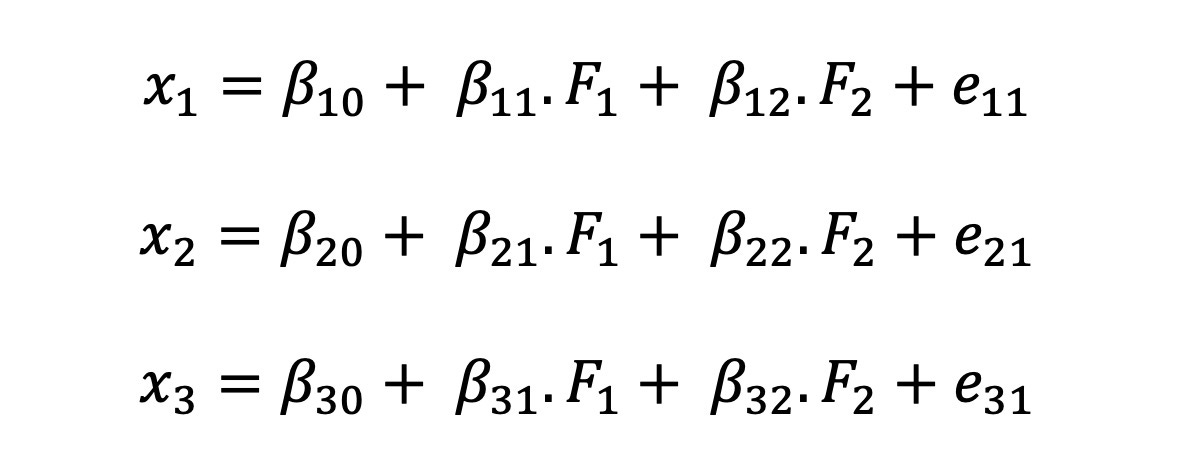
and so on for the remaining variables? (In this case, I have mentioned just two factors. Just make a note of that, we will revisit that soon).
Now, if I were to regress and identify F₁ and F₂, could you use them instead of x₁ to x₁₀? The answer is of course, YES!!. This is precisely the logic behind EFA. Now, how do we know that we have only two factors in our data? In all honesty, we don’t really know if we have two or twenty factors. That’s precisely the reason why we compute for various settings ranging from just one factor to as many as required to explain all the data. If you think about it a little bit, this number cannot be more than the number of variables you have in your data. What you do then is plot how much of the data is explained against the number of factors utilised in each setting. This is presented in the form of a elbow plot or scree plot . I’m appending a sample for you to observe just below.
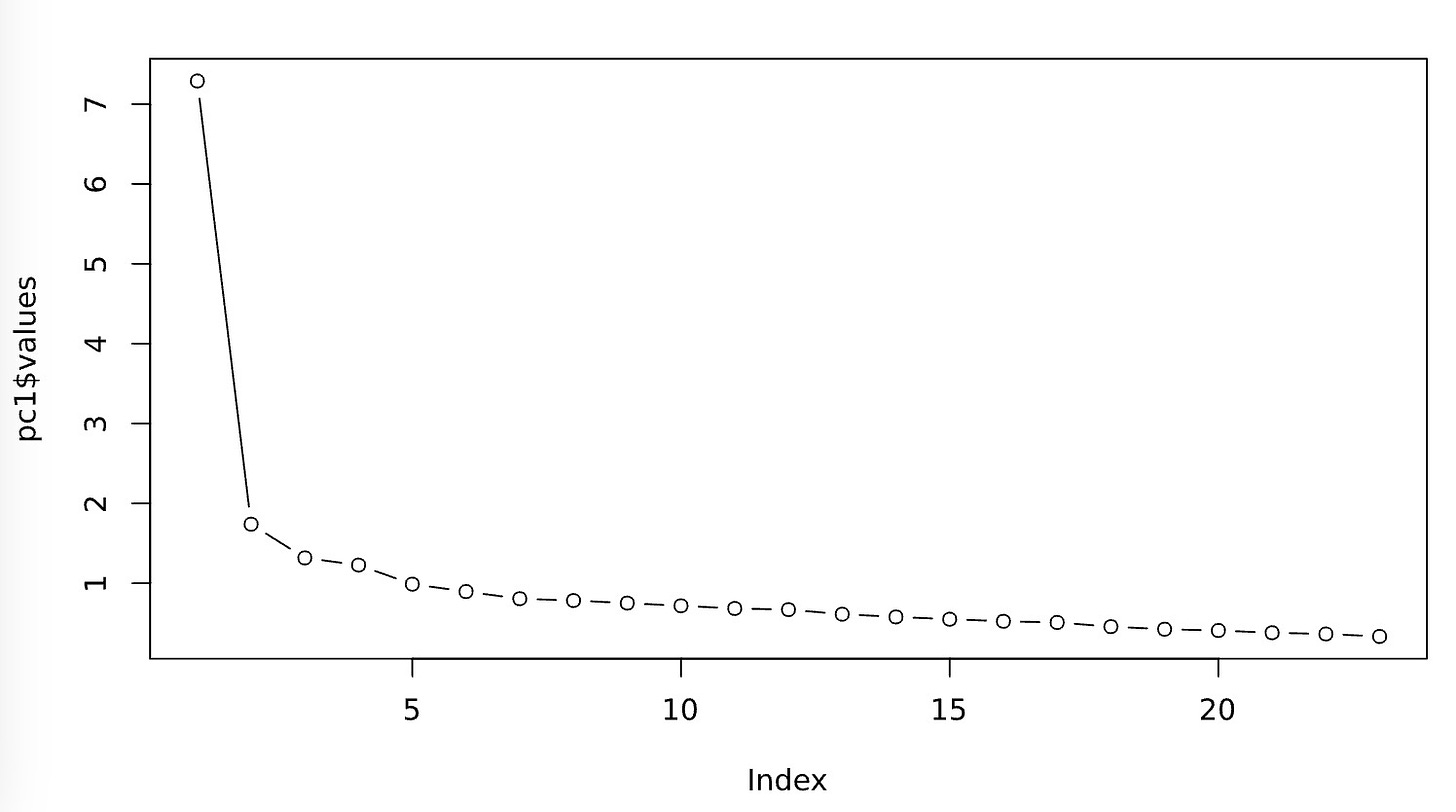
let’s just take a minute to understand why this is called a ‘scree’ plot. Turns out, these are naturally occurring land forms. According to WikiPedia, a Scree is a “collection of broken rock fragments at the base of a cliff or other steep rocky mass that has accumulated through periodic rockfall.” Here’s a picture of a scree formation in Nubra valley in Ladakh. I’ve also seen some on the way to Chakrata, a place that’s not very far from our campus

Coming back to the scree plot, in the x axis, you have number of factors. Basically, remember we assumed the presence of only F₁ and F₂ , that would be 2. If it was just F₁, then that’s 1. and you keep doing that cumulatively by adding more and more factors. Now, the interesting thing here is that each new factor that gets added explains less than the previous factors that were added. That sort of make intuitive sense if you think about it.
In the y axis, you find Eigen Values. Simply put, Eigenvalues represent the total amount of variance that can be explained by a factor (also principal component- but that’s beyond the scope of our discussion).
All this leads to the next important question- how many factors do we end up using? There is a bit of subjectivity in this department. Some scholars follow what’s called the ‘Kaiser's criterion’. (Kaiser in German means Emperor. I know there is a story there but I have not yet figured it out). Basically what that instructs is to select out the factors that have Eigenvalues under 1, that is remove out the factors that do not explain at least one variable completely. Others use the ‘elbow test’. Which is to find out where there Eigenvalues seem to level off and become parallel to the x axis. Both methods have their merits and demerits. If you are interested, you should dig deeper into this.
But for the purpose of our class, the idea is simple. After performing the exploratory factor analysis, we basically end up with factors that do a better job of explaining the variation in the data than the data itself. This helps us uncover ‘latent’ variables.
The same idea can also be used in something that researchers call Confirmatory Factor Analysis or CFA (not to be confused with the Chartered Financial Analyst programme). In the CFA, we basically freeze the number of factors before hand based on some hypotheses that we set. It is similar to checking if a certain variable is in fact a latent variable from the data that is presented to us. Researchers who are interested in building scales use both EFA and CFA in tandem to make scales are as reliable as possible. These tools are amongst the most commonly used ones in marketing research to understand customers better, design more effective advertisements, and uncover hidden relationships within variables. I’m positive that exploring the technique can help you while you are students too. For instance, a simple EFA and CFA combination can help you generate much better questionnaires. You can also check out from your own scores what factors have contributed to your success. Do think about them.
Let’s meet in class soon!
Good night!



